linear_data_structure

Linear Data Structures

Arrays

An arrays is linear data structure that stores elements in a contiguous space in memory. Each element in an array is identified by an index, allowing constant-time access to elements using their index.

This constant time access of element is possible due to the elements being stored in a contiguous manner. We can use pointer arithematic to find the element we wanna use with the index.

int arr[10] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};

For example when we do arr[5] we are saying to give the value stored at address of arr + (index * size of the data type) = &arr + (5 * sizeof(int)). Due to this the complexity of getting an element of an arrays is constant.

Properties

• Fixed Size - The size of a static arrays is fixed i.e. if we have declared a static arrays of size 10, we cannot increase the size of array and accessing the 11th element should give an out-of-bound error.
• Contiguous memory - Elements are stored sequentially in memory leading to constant time for finding and updating elements.

Types of arrays

• 1D arrays - A simple list of elements stored in a single row.

int arr[5] = {1, 2, 3, 4, 5};

• 2D arrays - A matrix like data structures useful for tabular data.

int matrix[3][3] = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
};

• nD arrays - An array that has more than two dimensions.

int arr[2][2][2];

Dynamic Arrays

A dynamic arrays is just like static arrays but they are resizable. A dynamic array maintain an underlying fixed-size arrays but doubles(depends on implementation) when it reaches capacity.

Dynamic arrays are heap allocated arrays that are made of three components:

• Pointer(&ptr) - A pointer to a heap allocated contiguous memory block that stores the elements
• Length(len) - The current number of elements stored in the array.
• Capacity (cap) - The total number of elements that can be stored in the allocated memory block until reallocation is needed.

Similar to arrays, dynamic arrays can be of any dimensions.

Some example of dynamic arrays are std::vector<T> - cpp , Vec<T> rust , list - py, etc

Some complexities

• Peek index - O(1)
• Update an index - O(1)
• insert at location - beginning - O(n), middle - O(n), end - O(1) amortized
• Resize - O(n)

Linked Lists

Linked lists are linear data structures that store data in nodes that point to one another, rather than in contiguous memory locations like arrays.

The nodes of a linked list are heap allocated and are made up of two components depending upon type of linked lists -

• Data - The data that must be stored
• Next - The pointer to next node.

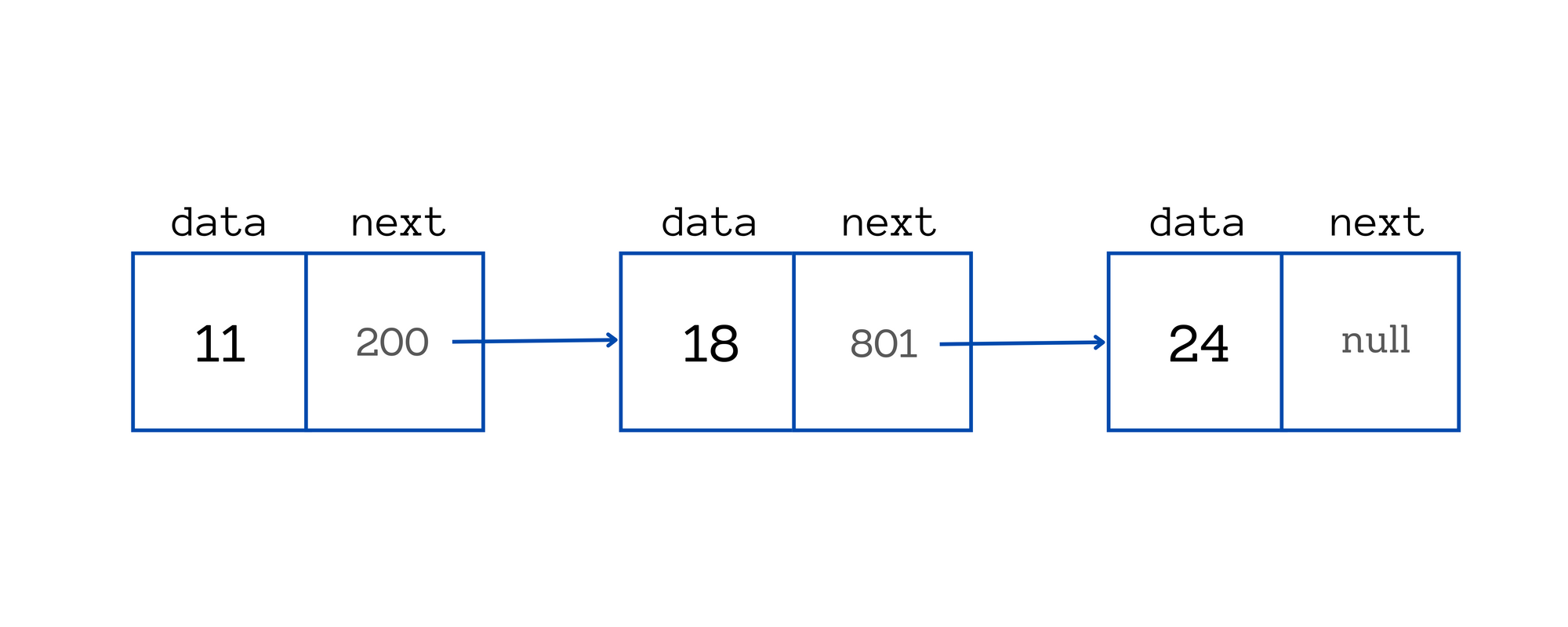
The first node of the linked list is called head and the last one is called tail.

Types of linked lists

There are various types of linked lists:

• Singly linked lists: In this type of linked list, the data is stored in the node and the node points to the next node.
• Doubly linked lists: In this type of linked lists, the node contains a pointer to both its previous and next node.
• Circular linked lists: In this type of linked lists, the last node points to the first node of the linked list.
• Doubly Circular linked lists: In this type of lists, the node pointer contains the address of previous and next node. The last node also points to the first node and the first node points to last node.

// NOTE PUT SOME COMPLEXITIES HERE.

Stack

A Stack is a linear data structure that follows the LIFO principle i.e. the last element pushed onto the stack is the first one to pop.

You can imagine a stack as a stack of objects in real life. If we have to put something on that stack we put it on the top and if we have to remove it, we remove the top one from the stack thus following the LIFO principle.

Key Operation

• Push - Pushing an element at top - O(1)
• Pop - Popping an element from the top - O(1)
• Peek - Peeking an element from the top - O(1)
• IsEmpty - Checking if the stack is empty - O(1)
• Size - Returning the size of stack - O(1)